基于类比法的多元函数微分学教学研究

高德超

摘? 要：类比思想是人类发现新知识的重要源泉，是人们提高学习和生活效率的一种方法，是培养创造性思维的一种途径.教学实践表明，类比法能够增加学生学习积极性，提高课堂教学效率，培养学生创新思维能力。多元函数微分学教學中科学地应用类比法，能够使抽象、复杂的多元函数问题转化为比较形象、简单的一元函数，在高等数学教学中起着十分重要的作用。

关键词：类比法? 一元函数? 极限? 多元函数

中图分类号：G642.0 ? ?文献标识码：A 文章编号：1672-3791（2019）10（a）-0107-03

随着我国经济的增长，在教育方面的大力投入，我国的高等教育已经完成了从精英教育到大众教育的转变，一定程度上满足了人们对高等教育的渴求，但是，这个快速的转变过程中也出现了一系列急需解决的问题，比如教学配套设施跟不上，学生水平参差不齐，新的学生培养方案没有跟上实际社会发展需求等问题;另外，2015年5月，国务院办公厅印发《关于深化高等学校创新创业教育改革的实施意见》，确立了创新精神、创业意识和创新创业能力为指标的人才培养要求。许多应用型本科高校积极响应政策号召，开始大量的增加实践科目的课时量，这对培养创新实践型人才的培养十分有利，但总的课时量却没有增加，大幅度减少数学、英语等基础学科的课时量成为必然，以某高校电气类专业为例，原来高等数学课时量为136学时，线性代数和概率统计课时量为64学时，而现在压缩到高等数学课时量为96学时，线性代数和概率统计课时量32学时，大量的课时压缩为数学课程的教学带来了很大的挑战。

对于大众化教育带来的问题，目前许多研究者已经从多角度进行了研究，赵文才等研究学者就当前大学生数学学习障碍成因进行了研究[1];杨孝平等研究学者就分层次教学法进行了研究[2];曾祥艳等研究学者就创新实践能力培养目标下的教学方法进行了研究[3]，这些方法对有效应对学生水平参差不齐问题，加大创新能力的培养等要求，但是，这些方法实施起来对课时量都有相对较多的要求.如何在较少的时间内完成高等数学保质保量的教学是亟待解决的问题，类比法的合理应用自然就成为了高等数学教学中重要方法。

1? 教学中类比法应用的必要性

类比法也称类比迁移，它是指人们在解决一个新问题时，往往与过去已经解决的相似的问题进行联系，用其解决已有问题的程序与方法去解决新问题.类比法是人们寻找发现真理的一种重要方法，例如，在万有引力定律的发现，牛顿就充分利用了自由落体与天体运动之间的类比;类比法也是培养创造性思维的一种途径，如鲁班发明锯子、德雷布尔制造潜艇等，类比法更是人们提高学习和生活效率的一种方法，正如德国古典哲学家康德所说：“每当理智缺乏可靠论证的思想时，类比这个方法往往指引我们前进[4]。”类比法在数学学科的教学的作用尤为重要，科学的将类比法应用于高等数学的教学中能够大大地提高教学效率，能够充分调动学生的学习积极性，加强学生的课堂参与度，培养学生的创新意识与创新能力。

2? 类比法的原则与步骤

应用类比法时应该遵循一定的基本原则，首先，类比的两问题之间应该有足够的相似性;其次，类比是在认知个体在已有知识体系的基础上进行的，即认知个体应拥有该问题领域足够的知识;最后，类比的结论要进行充分的论证，保证类比得出来的结论准确合理。

类比法的一般步骤：（1）明确研究的事物，即要明确知道研究目标（概念、性质或方法）是什么;（2）分析目的，提出问题，即分析要研究的事物要有什么样的基本特点，这些特点是否能与已知事物进行联系;（3）科学类比，得出结论，此时通过与已知事物进行联系类比，可得出类似的结论，验证类比结论的合理性。

3? 类比法在多元函数教学中的实践

高等数学中微分学部分的内容主要是由一元函数微分学和多元函数微分学两部分内容构成，两部分都有其固有的特点，一元函数微分学的内容我们易于数形结合的思路进行教学，内容相对直观简单易接受，但多元函数对应的维数较高，内容更加复杂，不易于作图或无法作图，这样直接进行教学就显得特别抽象，不利于学生学习，教学效果低下。此时，以一元函数微分学为基础，以类比法和翻转课堂为手段，以得到多元函数微分学相关的概念、性质与计算方法为目的，进行多元函数微分学的教学可以使教学更加形象易接受，将会大大地节约授课时间，提高教学效果，并且类比过程充分培养学生应用已有结论处理未知问题的能力，培养学生的创新意识。

类比法要求类比的两问题之间应有充足的表象相似性，为了满足相似性的需求，我们先引入多元函数的点函数形式：

u=f（P），P∈D（其中D∈Rk，k∈N）

此时，多元函数与一元函y=f（x）数的形式一致，从而可以利用类比方法得到多元函数中许多概念、性质和计算方法等。

3.1 类比法在多元函数概念中的应用

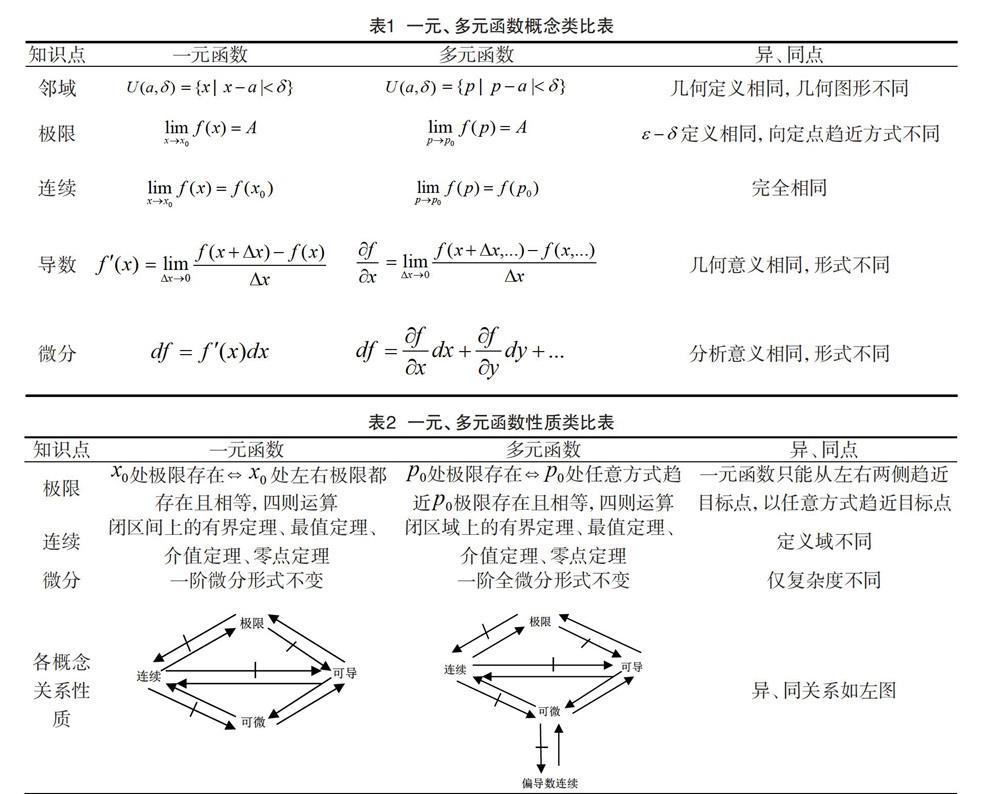
概念的学习是高等数学学习的基础，只有准确的理解掌握概念才能更好地进行后续的学习。概念的类比，需要概念本身既要有相同或高度相似的内涵，还要有形式的高度相似性，才能得到合理的概念，否则，类比得到的概念不能保证与标准概念的相容性;另外，针对类比得到的概念还要充分分析其与已有概念的相同点和不同点，这样既能加强学生对已有概念的记忆理解，又能促进学生对新概念本质的理解挖掘，避免因形式的相似而混淆相关的概念，一元函数、多元函数概念的类比可见表1。

3.2 类比法在多元函数性质中的应用

性质的学习是高等数学学习的核心，性质的正确理解应用是高等数学应用于其他学科前提，由于多元函数微分学中变量的增加，许多性质的严格证明复杂程度大大增加，并且多元函数的图像不易画，这样多元函数性质的学习理解难度大幅度增加，此时，多元函数的性质通过一元函数的性质进行类比讲解成为必然。通过这样的类比讲解，既能充分回顾复习一元函数的相关性质，加深对一元函数性质的理解，又能降低多元函数学习的难度，学生更容易接受。类比过程中，特别注意不同点的讲解，其中选取适当的反例的尤为关键。一元函数、多元函数性质的类比见表2。

3.3 类比法在多元函数解题中的应用

多元函数问题处理时一个重要的思路就是归化为一元函数，特别是多元函数极限问题处理，由于极限是微分学的基础，多元函数的求解显得十分重要，已经有许多对多元函数求解的方法[5]，虽然方法很多，但整体的思路还是利用类比归化为一元函数极限，充分利用一元函数极限求解的方法。

例 求极限。

分析：由于二元函数定义域是一个平面区域，→（0，0）的方式有无穷多中，没办法对此极限进行直接求解.从形式上看到应该应用四则运算，且分子与分母中都含有项，应该归化类比于一元函数。

解 原式

（其中）=0

4? 结语

实践教学表明，类比法能够加大学生对教学过程的参与度，增加学生学习积极性，提高课堂教学效率，培养学生创新思维能力，科学地应用类比法，能够使是抽象的问题形象化，复杂问题简单化，未知问题已知化，在高等数学教学中起着十分重要的作用。但是，类比法应用时必须要遵循类比法的原则，类比得出的结论应该有充分的论证，不能盲目乱用。

参考文献

[1] 赵文才，侯婷，杨记明，等.大学数学学习障碍的成因与对策[J].教育与教学研究，2010，24（8）：112-114.

[2] 杨孝平，俞军，陈萍，等.深化分层次教学提高大学数学教育质量[J].中国大学教学，2006（3）：14-16.

[3] 曾祥艳，南江霞.基于创新实践能力培养的大学数学教学改革研究[J].黑龙江教育：高教研究与评估，2017（5）：39.

[4] 章士藻.数学方法论简明教程[M].南京：南京大学出版社，2006.

[5] 冯英杰，李丽霞.二元函数极限的求法[J].高等数学研究，2003，6（1）：32-33.

编辑整理：科学技术创新杂志社编辑部 官方网站：www.hljkxzzs.com