[电气与信息工程]基于GBDT的串联结构微电网与电网交互稳定性评估

张津京 王兴贵 宋汶秦 杨维满

摘? ?要：针对微源逆变器串联微电网中，微源投切对微电网与电网交互稳定性影响机理复杂，传统方法建模困难且无法及时决策的问题，提出一种基于梯度提升决策树（gradient boosting decision tree，GBDT）模型的交互稳定性评估方法.首先提出微源投切特征函数的构造方法，所提方法能够有效提取采用载波移相SPWM调制的串联结构系统中特有的投切微源位置特征，同时具有降低特征维数、提高模型效率、通过简单拟合使模型具备迁移能力的优势;其次将交互稳定性评估视为多分类任务，且对其中较不稳定样本进行谐振频段预测，从而可针对不同投切工况采取不同应对策略.在验证集和新建测试集上的测试结果表明特征提取方法正确、有效，可为类似串联结构系统在电能质量分析、优化运行等方面提供方法参考;所建模型泛化能力强且具有实用性，可为并网运行系统稳定性在线分析及决策提供新思路.

关键词：微源投切;微源逆变器串联;交互稳定性;特征提取;机器学习

Abstract：Due to the complex mechanism of the effect of micro-source switching on interactive stability between the grid and the micro-grid with series micro-source inverters， traditional methods were difficult to model and can't make decision in time. In this study， therefore， an assessment method of interactive stability based on gradient boosting decision tree （GBDT） was proposed. Firstly， the feature functions of the micro-source switching were constructed to extract the position feature which existed typically in series structure system modulated by carrier phase shifted SPWM. The proposed functions can reduce the feature dimension， thus improving the efficiency of assessment model and making the model migration capable by feature fitting. Secondly， the assessment of interactive stability was treated as a multi-classification task and the resonant frequency bands of instable samples were predicted. Thus， the different strategy can be taken according to the classification and prediction. Finally， the tests on validation data sets and new test sets verified the correctness and effectiveness of the feature construction functions which can provide references for the similar series structure system in power quality analysis， optimal operation and other aspects. The results also verified the high generalization performance and practicality of the proposed assessment model， which can provide a new tool for on-line stability analysis and decision-making of grid-connected operation systems.

Key words：micro-source switching;series micro-source inverters;interactive stability;feature extraction;machine learning

微電网是分布式电源（distributed generation，DG）接入电网的一种有效手段.相比于DG和负荷在馈线上横向分布的并联结构微电网，本文讨论的微源逆变器串联微电网（micro-grid with series micro source inverters，SMSI-MG）输出的电压和电流具有更好的正弦度，同一输出电压等级下可有效降低各微源直流侧电压[1-3]. 类似的逆变器串联结构因其高输出电压、低dv/dt、高效率等优势而在光伏并网系统中获得广泛应用[4-5]. SMSI-MG系统则在此基础上将不同类型的DG进行整合，可进一步提高可再生能源利用率.

目前，微电网中的大部分电源均为使用并网变流器作为接口的DG，在并网运行时会由于变流器的高频开关特性而产生大量谐波，污染电网.进一步地，变流器与变流器之间、变流器与电网之间的谐波交互作用也可能引起谐振，导致网侧电压/电流谐波幅值持续放大、严重畸变，进而造成保护装置误动、变流器控制环失稳等，严重影响系统的安全稳定运行[6-7].? 这种变流器接入电网后的谐波不稳定现象早在2014年就引起了丹麦Aalborg大学F. Blaabjerg课题组的关注[8-9]. 之后，国内外学者对谐波振荡引起的交互系统稳定性问题进行了大量研究[10-11]，但主要针对弱电网环境下的单台逆变器或多台逆变器并联的系统，对SMSI-MG这种微源逆变器（micr-source inverter，MSI）串联的系统研究较少. SMSI-MG中MSI与MSI之间、串联的MSI与电网之间同样存在谐波交互作用.特别地，当微源因故障或出力受限进行投切操作后，SMSI-MG与电网之间的交互作用更加明显，也更加复杂. 由于谐波振荡引起的交互系统不稳定具有一定的危害性，因此对其提前进行估计和防范具有重要意义.

从研究方法来说，目前对并网运行系统稳定性进行分析时主要采用状态空间法[12-13]和阻抗分析法[14-15]. 然而时频域的分析方法存在模型复杂、计算速度慢、实时性差等问题，无法在微源投切后短时间内进行分析决策. 近年来，基于数据的机器学习在电力系统暂稳评估研究中取得了重大进展[16-17]. 机器学习方法将稳定性评估看作一个分类问题，通过离线自动学习建立物理量与稳定后果之间的映射关系.集成学习方法则将几种机器学习技术组合成一个预测模型，可减小方差，改进预测效果[18]. 其中，基于树模型的集成学习方法梯度提升决策树GBDT更是在Kaggle、KDD （knowledge discovery in database） 等一系列数据挖掘竞赛中受到广泛关注.考虑到微源投切对SMSI-MG和电网交互稳定性影响机理不明、传统方法无法及时决策等问题，本文借鉴现有电力系统暂稳评估思想，提出一种基于GBDT的交互稳定性影响评估方法.在建立机器学习模型时，特征提取是关键.因此首先通过分析微源投切与系统输出电压之间的关系，提出特征提取和构造方法.该方法同时考虑到了系统拓扑结构发生变化时所建模型的适应能力，通过简单地拟合即可使模型适应于新网络拓扑，具备良好的泛化性能.最后对所建模型进行了测试.

1? ?微源投切特征构建及稳定性分级

图1为并网运行模式下SMSI-MG系统拓扑.风力、光伏等微源直流侧配备储能装置，通过对其有效控制可抑制功率波动从而保证各MSI直流侧电压相等. H桥MSI输出端串联，系统输出的多电平电压经简单滤波后即可具有较好的正弦度.正常运行时，单相微源数目为n.三相系統由单相系统组合而成. 为描述方便，将单相包含n个微源的三相SMSI-MG系统简记为n-SMG.该系统在公共耦合点（point of common coupling，PCC）处接入电网. 采集PCC处电压电流经控制器和载波移相SPWM调制（carrier phase shifted SPWM，CPS-SPWM）后实现对各MSI的控制，从而使系统输出满足电网调度和负荷需求.微源投切通过开合开关SC实现.

1.1? ?输入特征构建

利用机器学习训练交互稳定性评估模型，就是要建立输入特征与交互稳定状态的映射关系，因此输入特征的选取和构建是首要的步骤.在对微源投切引起的交互稳定性影响进行评估时，若将三相所有微源的投切状态作为特征属性，则对于一个n-SMG系统，仅该部分特征维数就为3n.遍历各种投切工况将产生“组合爆炸”问题，而在设置训练样本时则易出现大量相似或是遗漏工况，导致训练模型欠拟合、泛化性能差. 为避免上述问题，本文对投切工况Sl（l = 1，2，…，L）构造如下特征函数：

1）三相微源平均投切率

投切微源的数目直接影响运行微源的数目，进而影响系统输出电压中基波和谐波的含量.为使模型具备迁移能力，定义投切工况Sl对应的A相切除微源比例为δac，恢复投入的微源比例为δap，则δap≤δac. 令δa = δac - δap为A相微源投切率，其余两相同理.由于A、B、C三相微源投切对交互系统稳定性的影响是等价的，因此为了弱化具体相特征对模型泛化能力的影响，定义工况Sl对应的三相微源平均投切率为

表1中，数据①为切除2个微源的情况，其中一个为MS1，另一个则相对MS1的位置不同.由式（1）、（2）可知5种Sl下αl和βl相同. 但5组求和结果的方差较大，由于此时式（3）中其他变量相同，因此可知被切除微源之间的相对位置不同时，uo差异较大.数据②、③进一步说明了这一点. 由此可以推断对于n-SMG系统，当αl和βl相同时，若投切微源之间的相对位置不同，则系统输出电压电流中的谐波含量差异较大，其对交互稳定性的影响程度必然不同.这是采用CPS-SPWM调制的串联结构系统中特有的现象.因此投切微源的位置应当作为一个与投切数目同样重要的输入特征参与交互稳定性的评估.

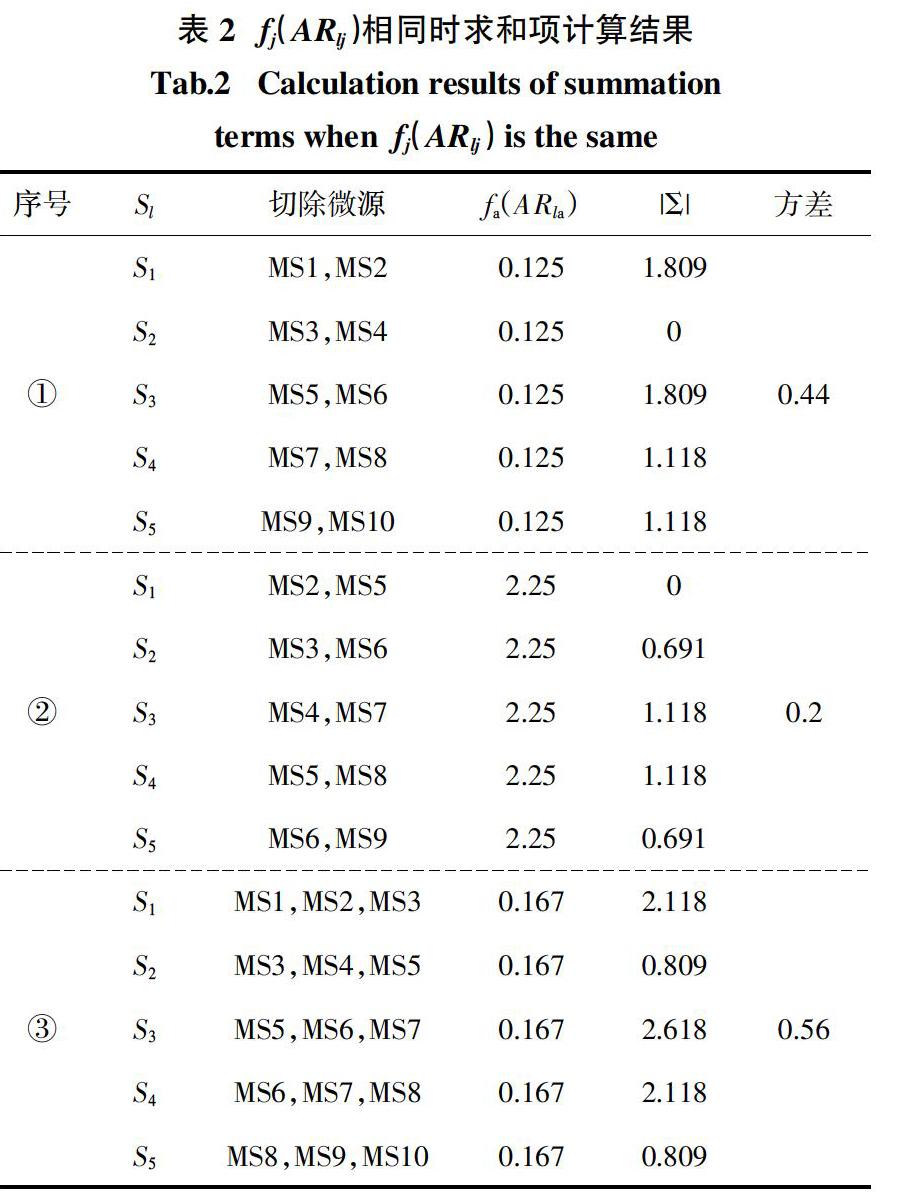
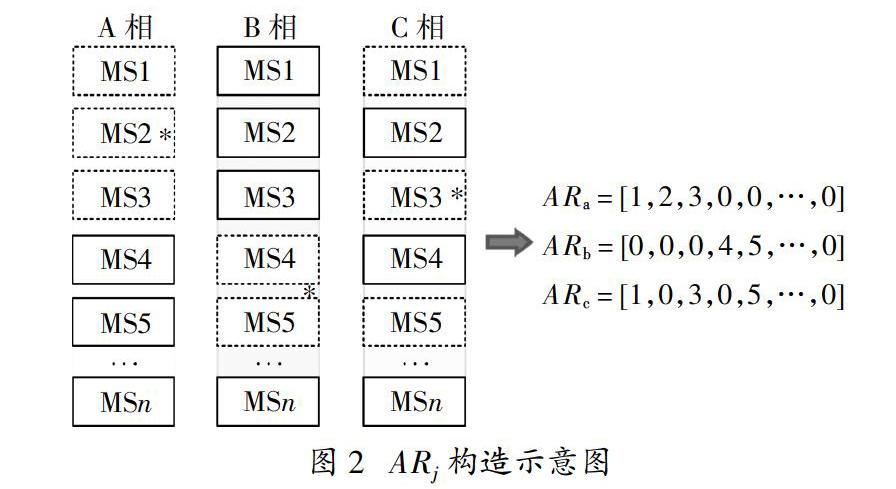
为提取工况Sl对应的j相投切微源之间的相对位置特征，首先构造投切数组ARlj. 如图2所示，微源仍按其MSI串联顺序标记为MS1、MS2 、…、MSn.切除微源在图中用虚线框表示，如A相的MS1、MS2和MS3. 对应于ARlj中，将其序号i列出，而未切除的微源则标记为0，故此时ARla = [1，2，3，0，0，…，0]，其余与之同理.在获得ARlj后，构造对应的离散度函数用于表征投切微源之间的相对位置.该离散度函数应当满足：1）投切微源之间相对位置变化规律相同则离散度相同;2）δj相同的情况下，切除连续序号的微源越多则离散度越小.据此构造如下所示工况Sl对应的j相投切微源离散度函数为? 表2中，数据①为切除连续2个微源的情况，5种Sl下被切除微源之间相对位置相同，因而由式（4）计算得到的离散度相同. 数据②和③同理.但三组数据求和结果方差均较大，这说明即便投切微源数目相等、相对位置相同，uo还会因为投切微源的绝对位置不同而产生较大差异，因此需要进一步补充其他特征对其进行区分. 观察表2中各Sl发现，αl、βl和γl相同的情况下，投切微源中心μ是不同的，故利用离散度结合中心点的方式即可较好地表征及区分不同的微源投切位置.显然该方法可推广至n-SMG系统及类似采用CPS-SPWM调制的串联结构系统.为了进一步降低特征维数，定义工况Sl对应的三相微源投切中心欧式距离为

对于一个投切工况Sl，通过上述四个特征即可获取其对应的投切微源数目和位置信息，且特征维数从3n个投切状态减少为4个，这对提高模型训练效率有重要作用.

1.2? ?交互稳定性分级

基于阻抗的并网系统稳定性研究表明，并网运行系统阻抗与电网阻抗之间的动态耦合决定了交互系统的稳定性.当两者阻抗幅值相交处相位裕度较小或过大时，交互系统易出现阻抗交点频率附近的特定次谐波振荡，从而导致交互系统不稳定，而此时并网电流中相应谐波分量会因此而表现为增大至超过其限值 [14-15，20-22]. SMSI-MG中微源投切后，其输出阻抗必然发生改变，在假设运行环境其他参数不发生变化的情况下，交互系统稳定性、并网电流谐波分量都会因此而发生改变. 为避免复杂的序阻抗测量及相位裕度计算，本文通过提取并网电流中的谐波分量衡量交互系统稳定性. 同时，为了充分利用机器学习处理多分类任务的优势，不同于传统方法仅有稳定和不稳定两个状态，本文在稳定和不稳定之间设置临界状态，从而对交互系统稳定性进行更细致和直观的划分.

假设投切工况Sl时PCC处三相电流中谐波分量为Thl，按照我国GB/T 14549—1993电能质量标准要求所得谐波电流分量的标准值为Thl-sta，定义各次谐波超限比为ξhl = （Thl-Thl-sta）/Thl-sta;依据ξhl将交互系统稳定性划分等级如下 式中：h代表谐波阶次;ξlow1、ξlow2为设定的25次以下谐波电流超限比阈值;ξhig1、ξhig2为25次以上谐波电流超限比阈值;Wl = 1时谐波电流分量均在限值以下，说明交互系统稳定裕度充足，系统稳定，该种投切工况不会对系统安全稳定运行造成影响;Wl = 2表示较稳定，此时特定次谐波电流分量有较小幅度的增加，交互系统可能存在轻微谐振;Wl = 3时特定次谐波电流分量超过限值较多，说明交互系统稳定裕度低，系统进入不稳定状态. 为与Wl = 4区分，称此时为较不稳定等级，这时通过调整控制方式可对Sl引起的谐波振荡进行抑制;Wl = 4时特定次谐波电流含量超过50%，交互系统失稳，且并网电流严重畸变，在系统运行过程中应禁止出现该种投切工况.

为了有针对性地调整较不稳定情况下的控制策略，及时抑制或消除微源投切引起的谐振，对该谐振的频率范围进行预测是有必要的. 对此，将Wl=3的样本对应的谐波频段作为预测目标，构建如下分类器.

2? ?用于交互稳定性评估的GBDT算法

2.1? ?GBDT分类算法

梯度提升决策树[23]（GBDT）是一种基于决策树的集成学习方法，其基本思想是每轮迭代中通过拟合残差来学习一个CART回归树模型T（x;θm），使得损失函数逐步减小.

对于具有K个类别的训练样本，GBDT学习算法框架如图3所示. 采用One vs Rest （OvR）分类方法将类别进行one-hot编码，对每个编码输出分别建立决策树进行迭代. 有监督的机器学习通常通过损失函数衡量预测值与真实值之间的偏差，模型训练的目标是损失函数值尽可能小. 多分类GBDT学习算法采用对数损失函数，即? ?该误差是样本l对应类别k的真实标记和t-1轮GBDT预测概率的差值，即残差. 为使损失函数进一步减小，将（xl，r （t-1），k）作为第t轮、第k个分类器中决策树的训练数据，如此迭代，直到模型准确度无法再提高时停止，获得最终的GBDT模型.

为防止过拟合，通过正则化项及子采样的方式提高模型泛化能力.其中，正则化项通过为每个弱学习器加上权重缩减系数v，弱化单个学习器的效果，从而提高模型整体的性能.加入正则化项后GBDT模型第t轮迭代输出為;? ?另外，GBDT模型中弱学习器之间存在依赖关系，其训练过程是串行进行的，但通过无放回抽样可实现部分并行训练，从而提高模型泛化能力及训练效率.

2.2? ?SMOTE过采样

微源投切后交互系统中稳定和失稳样本较少，类别比例不平衡，这将导致分类结果准确率较低.对此，本文采用合成少数类过采样（synthetic minority oversampling technique，SMOTE）方法[24]使原始数据中的类别比例更合理.该算法采用kNN方法在少数类样本的k个近邻中随机挑选N个样本进行随机线性插值，并与原数据合成产生新样本.

图4为部分样本采用SMOTE方法前后的类别分布对比图.其中，原始样本中Wl = 1的样本比例为11.7%，Wl = 3的样本占到51%，Wl = 4的样本则仅占7.3%.经过SMOTE处理之后，原本占比较少的类别1和3的样本分别在其k近邻内通过插值产生了与其类别一致的新样本，从而使得这两类样本数量明显增多，最终3类样本比例趋于平衡.

2.3? ?评价指标

交互稳定性分析中，若将较不稳定和失稳样本（Wl = 3，Wl = 4）错判为稳定，将导致交互系统失稳前运行人员不采取任何控制或禁止措施，从而给系统造成严重破坏. 相比较而言，此种误判比将稳定样本误判为失稳样本带来的影响要大得多. 因此，模型评价指标除考虑准确率Acc外，还更加关注较不稳定和失稳样本的精度、召回率以及F1值. 多分类器混淆矩阵如表3所示.

3? ?仿真分析

3.1? ?样本生成

通过对10-SMG系统中各种预想投切工况进行大量仿真，获取样本数据. 仿真中，为保证投切前后并网运行电流方向不变，取αl ≤ 43.3%.另外，以初始状态为基准，设定电网阻抗和滤波电感变化范围为±25%.控制器采用准比例谐振，其比例系数变化范围为0.01～0.5.谐波电流超限比阈值设定为：ξlow1= 1.2，ξlow2=8，ξhig1=1.5，ξhig2=45.经过筛选后获取1 000组样本数据，并以其中70%作为训练样本集，30%作为验证样本集.

3.2? ?不同模型仿真结果对比

为验证模型评估和预测效果，将GBDT模型与其他常用机器学习模型的评估结果进行对比.测试模型均基于开源机器学习库Scikit-learn搭建[25]. 参数使用五折交叉验证的方法获取最优值，GBDT模型的正则化通过超参数n_estimators、learning_rate和subsample实现;支持向量机（SVM）使用多项式核函数.采用式（12）～（18）定义的评价指标，得到验证集上的测试情况如表5所示.其中，GBDT表示使用未经SMOTE处理的训练数据得到的模型，除此之外的模型均采用过采样后的样本数据;谐振频段预测则使用原始样本中Wl = 3的样本.

表5中，GBDT和RF为集成学习器，其余为个体学习器. 对比发现，集成学习器总体比个体学习器拥有较高的准确率;同样是集成学习器，RF和GBDT准确率相同，但GBDT在类别3上具有较高的F1值，且谐振频段预测准确率较高. 未经过采样的GBDT模型评估准确率最低，可见样本类别平衡对提高模型准确率有重要作用，由此也证明了结合过采样方法的必要性和有效性. 总体看来，结合SMOTE的GBDT模型可实现交互系统稳定性和谐振频段较高准确率的评估和预测，这也从另一个方面说明了特征提取方法的正确性.

3.3? ?模型迁移能力验证

为验证所建模型的适应性，设置微源数目n从5至40以5为步长变化，分别建立n-SMG并网运行系统仿真模型，且新拓扑系统保持与10-SMG直流侧总电压相等. 各系统分别对30种不同投切Sl进行仿真构成240个新建测试样本.由于微源数目n不同，在利用式 （5）、（6）计算投切微源位置特征属性值时，会出现与10-SMG系统规律相同但属性值不同的情况，使得之前构建的GBDT模型应用于n-SMG（n≠10）系统时会发生误判. 因此对于n-SMG（n≠10）系统，首先需要对特征γ和d进行映射，使其与10-SMG的数值相对应.

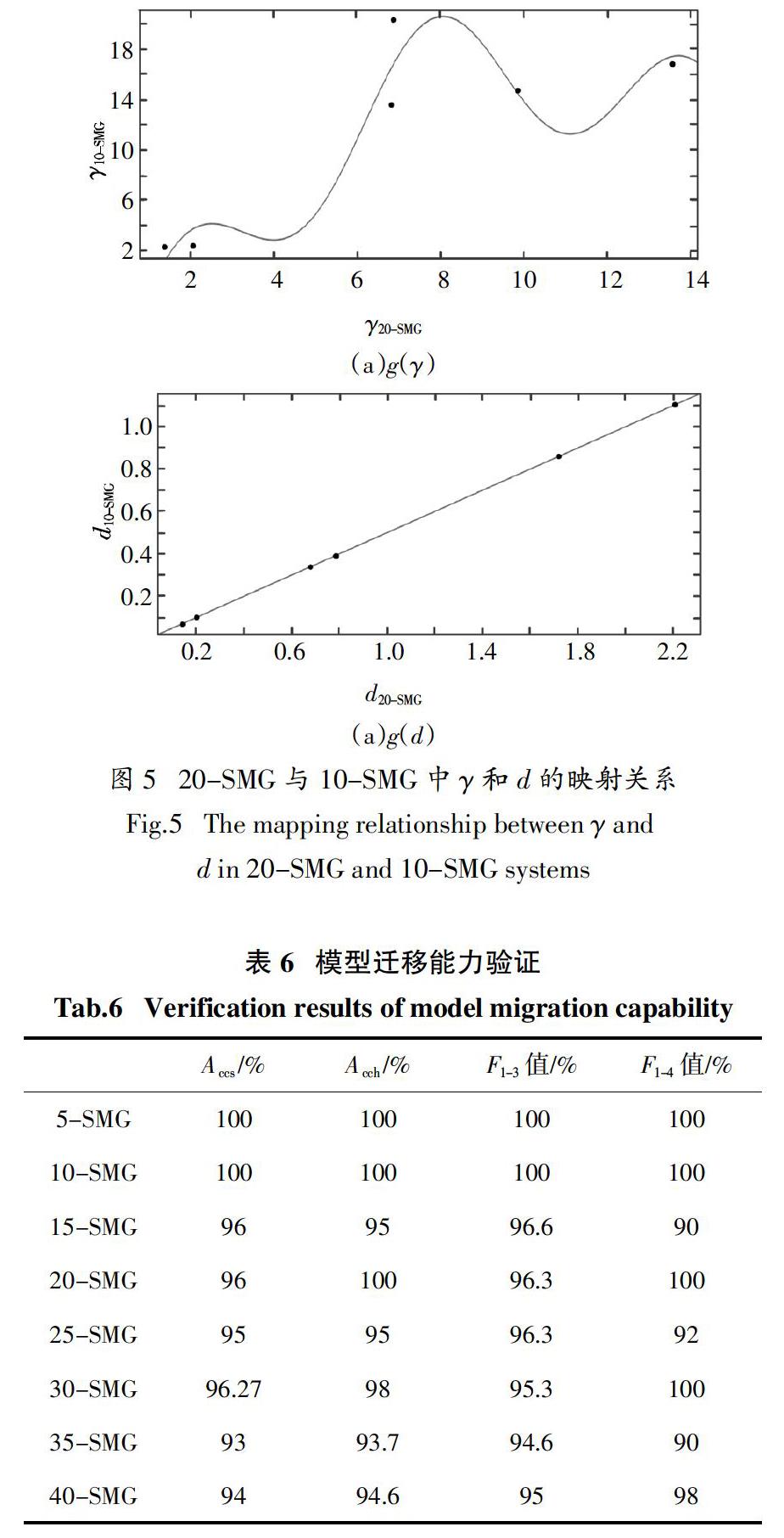
选取若干具有代表性的点对[xn - SMG，x10-SMG]，通过线性拟合获得新拓扑系统和10-SMG在特征X下的对应关系g（X），如图5所示的20-SMG与10-SMG系统中的g（γ）和g（d）. 之后将g（X）应用于新拓扑下的其他样本，即可获得映射后的特征属性值.通过该映射方法，分别得到n-SMG修正后的特征值，通过之前所建GBDT模型进行交互稳定性分级评估和谐振频段预测，验证结果如表6所示. 其中10-SMG的投切样本是原始样本中未出现的投切工况.

从表6可看出，所建模型应用于5-SMG和10-SMG时，测试准确度较高. 而应用于n>10的系统时，由于γ的非线性映射以及训练样本的缺失，准确率有所下降，但后期通过补充样本可望进一步提高准确率. 总体来看，所建模型通过特征属性的简单拟合即可适用于新拓扑系统，避免花费大量时间重新生成样本，具有一定的实际应用价值.

基于GBDT的交互稳定性评估主要由离线训练和在线评估两部分构成. 通过前期数据集生成、离线模型训练和模型性能评估，可获得训练好的GBDT模型.在线评估时通过在线获取微源投切等特征数据，并将特征数据输入（根据系统拓扑结构，映射或直接输入）训练好的模型，即可对相应投切操作引起的交互稳定性进行评估，并预测谐振频段，为预防控制提供及时有效的决策依据.

4? ?结? ?论

本文将机器学习用于微源投切后的SMSI-MG与电网交互稳定性分析，提出一种适用于串联结构系统的微源投切特征提取方法，并采用GBDT模型进行交互稳定性评估和谐振频段预测. 得到如下结论：

1）对于采用CPS-SPWM调制的并网运行SMSI-MG系統，其与电网的交互稳定性不仅与投切微源数目相关，还与投切微源的位置相关. 通过三相微源平均投切率、投切不平衡度、投切平均离散度、投切中心欧式距离四个特征函数即可提取三相投切微源的数目和位置信息.而通过对后两者的拟合，模型即可具备良好的泛化和迁移能力.特征提取方法正确，模型训练效率高.

2）将微源投切对交互系统稳定性的影响划分为4个类别，类别划分更细致，且对较不稳定样本中的谐振频率范围进行预测，避免了传统方法中的谐振检测. 模型输出为多类别、多标签，对后续决策更具实时性和指导性.

3）采用结合过采样的集成学习方法，与其他个体学习器的评估方法相比，保证了较高的总体评估和预测准确性. 模型泛化能力强，具有实用价值.

本文所提基于机器学习模型的交互稳定性评估方法无需建立复杂的数学模型，为并网运行系统稳定性在线分析及决策提供了新思路，同时所提出的特征提取方法也可为类似串联结构系统在电能质量分析、优化运行等方面提供方法参考. 在今后的研究中，除进一步扩大样本规模外，还需寻找更优的指标将微源投切对交互系统的影响量化呈现出来，以进一步提高模型的实际应用价值.

参考文献

[1]? ? YANG W M，WANG X G，LI X Y，et al. An active power sharing method among distributed energy sources in an islanded series micro-grid[J]. Energies，2014，7（12）：7878—7892.

[2]? ? 杨维满，王兴贵. 串联结构中H桥逆变器直流侧等效模型关系[J]. 电工技术学报，2015，30（16）：103—110.

YANG W M，WANG X G. Relationship of DC-side equivalent model among H-bridge inverters connected in series[J]. Transactions of China Electrotechnical Society，2015，30（16）：103—110. （In Chinese）

[3]? ? 王兴贵，杨维满.孤岛模式下串联型微电网逆变系统动态建模[J]. 高电压技术，2014，40（8）：2456—2463.

WANG X G，YANG W M. Dynamic modeling of inverter system in isolated series micro-grids[J]. High Voltage Engineering，2014，40（8）：2456—2463. （In Chinese）

[4]? ? XIAO B L，HANG L J，MEI J，et al. Modular cascaded H-bridge multilevel PV inverter with distributed MPPT for grid-connected applications[J]. IEEE Transactions on Industry Applications，2015，51（2）：1722—1731.

[5]? ? GE B M，LIU Y S，ABU-RUB H，et al. State-of-charge balancing control for a battery-energy-stored quasi-Z-source cascaded-multilevel-inverter-based photovoltaic power system [J]. IEEE Transactions on Industrial Electronics，2015，65（3）：2268—2279.

[6]? ? SHUAI Z K，LIU D G，SHEN J，et al. Series and parallel resonance problem of wideband frequency harmonic and its elimination strategy[J].IEEE Transactions on Power Electronics，2014，29（4）：1941—1952.

[7]? ? 劉怀远，徐殿国，武健，等. 并网换流器系统谐振的分析、检测与消除[J]. 中国电机工程学报，2016，36（4）：1061—1074.

LIU H Y，XU D G，WU J，et al. Analysis，detection and mitigation of resonance in grid-connected converter systems[J]. Proceedings of the CSEE，2016，36（4）：1061—1074.（In Chinese）

[8]? ? WANG X F，BLAABJERG F，WU W M. Modeling and analysis of harmonic stability in an AC power-electronics-based power system[J].IEEE Transactions on Power Electronics，2014，29（12）：6421—6432.

[9]? ? WANG X F，BLAABJERG F，LOH P C. Grid-current-feedback active damping for LCL resonance in grid-connected voltage-source converters[J]. IEEE Transactions on Power Electronics，2016，31（1）：213—223.

[10]? 朱晓娟，胡海涛，陶海东，等. 光伏并网系统的谐波不稳定产生机理及影响规律[J]. 电工技术学报，2017，32（10）：33—41.

ZHU X J，HU H T，TAO H D，et al. The mechanism and influence of harmonic instability for photovoltaic grid-connected system[J]. Transactions of China Electrotechnical Society，2017，32（10）：33—41. （In Chinese）

[11]? HARNEFORS L，WANG X F，YEPES A G，et al. Passivity-based stability assessment of grid-connected VSCs-an overview[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics，2016，4（1）：116—125.

[12]? KWON J，WANG X F，BAK C L，et al. Harmonic interaction analysis in grid connected converter using Harmonic State Space （HSS） modeling[C]//2015 IEEE Applied Power Electronics Conference and Exposition （APEC）. Charlotte，NC，USA：IEEE，2015：1779—1786.

[13]? BOTTRELL N，PRODANOVIC M，GREEN T C. Dynamic stability of a microgrid with an active load[J]. IEEE Transactions on Power Electronics，2013，28（11）：5107—5119.

[14]? SUN J.Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics，2011，26（11）：3075—3078.

[15]? 陈新，张旸，王赟程. 基于阻抗分析法研究光伏并网逆变器与电网的动态交互影响[J]. 中国电机工程学报，2014，34（27）：4559—4567.

CHEN X，ZHANG Y，WANG Y C.A study of dynamic interaction between PV grid-connected inverters and grid based on the impedance analysis method[J]. Proceedings of the CSEE，2014，34（27）：4559—4567. （In Chinese）

[16]? 石訪，张林林，胡熊伟，等. 基于多属性决策树的电网暂态稳定规则提取方法[J]. 电工技术学报，2019，34（11）：2364—2374.

SHI F，ZHANG L L，HU X W，et al. Power system transient stability rules extraction based on multi-attribute decision tree[J]. Transactions of China Electrotechnical Society，2019，34（11）：2364—2374. （In Chinese）

[17]? 周挺，杨军，周强明，等. 基于改进LightGBM的电力系统暂态稳定评估方法[J]. 电网技术，2019，43（6）：1931—1940.

ZHOU T，YANG J，ZHOU Q M，et al. Power system transient stability assessment method based on modified LightGBM[J]. Power System Technology，2019，43（6）：1931—1940. （In Chinese）

[18]? 张晨宇，王慧芳，叶晓君. 基于XGBoost算法的电力系统暂态稳定评估[J]. 电力自动化设备，2019，39（3）：77—83.

ZHANG C Y，WANG H F，YE X J. Transient stability assessment of power system based on XGBoost algorithm[J]. Electric Power Automation Equipment，2019，39（3）：77—83. （In Chinese）

[19]? 周京华，陈亚爱. 高性能级联型多电平变换器原理及应用[M].北京：机械工业出版社，2013：87.

ZHOU J H，CHEN Y A. Principle and application of high performance cascaded multilevel converter [M]. Beijing：China Machine Press，2013：87. （In Chinese）

[20]? CESPEDES M，SUN J. Impedance modeling and analysis of grid-connected voltage-source converters[J]. IEEE Transactions on Power Electronics，2014，29（3）：1254—1261.

[21]? 王赟程，陈新，陈杰，等. 基于谐波线性化的三相LCL型并网逆变器正负序阻抗建模分析[J].中国电机工程学报，2016，36（21）：5890—5898.

WANG Y C，CHEN X，CHEN J，et al. Analysis of positive-sequence and negative-sequence impedance modeling of three-phase LCL-type grid-connected inverters based on harmonic linearization[J]. Proceedings of the CSEE，2016，36（21）：5890—5898. （In Chinese）

[22]? CHO Y，HUR K，KANG Y C，et al. Impedance-based stability analysis in grid interconnection impact study owing to the increased adoption of converter-interfaced generators [J]. Energies，2017，10（9）：1355—1372.

[23]? FRIEDMAN J H. Greedy function approximation：a gradient boosting machine[J]. Annals of Statistics，2001，29（5）：1189—1232.

[24]? CHAWLA N V，BOWYER K W，HALL L O，et al. SMOTE：synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research，2002，16：321—357.

[25]? PEDREGOSA F，VAROQUAUX G，GRAMFORT A，et al. Scikit-learn：Machine learning in Python[J]. Journal of Machine Learning Research，2011，12：2825—2830.

编辑整理：科学技术创新杂志社编辑部 官方网站：www.hljkxzzs.com