[]不同体积掺量的钢纤维在混凝土中的分布研究

毕继红　赵云　鲍春　霍琳颖　王照耀　乔浩玥

摘 ? 要：为研究不同体积掺量的钢纤维对钢纤维自密实混凝土中纤维分布和取向的影响，配制了4种不同纤维体积掺量的纤维自密实混凝土，首先探究了新拌混凝土的流变性质与纤维体积掺量之间的关系，同时分析了梁试件切割面上的纤维分布. 考虑纤维体积掺量对新拌混凝土流变性质的影响，采用ANSYS CFX软件模拟了具有4种不同纤维体积掺量的新拌混凝土的流动. 基于模拟得到的混凝土速度场，将纤维视为刚性连接的数个球形粒子，通过求解刚体动力学方程计算了纤维的运动. 通过与试验结果对比发现，本文提出的模拟方法能较好地确定纤维在混凝土中的分布与取向;模拟结果表明，随着纤维体积掺量的增加，纤维在梁竖直方向的离析程度减小，相反地，纤维与梁轴向的取向角度增大.

关健词：纤维体积掺量;纤维分布;纤维取向;混凝土的流变性;数值模拟

中图分类号：TU528 ? ? ? ? ? ? ? ? ? ? ? ? ?文献标识码：A

Research on Distribution of Steel Fiber with Different

Volume Content in Concrete

BI Jihong1，2?，ZHAO Yun1，BAO Chun3，HUO Linying1，WANG Zhaoyao1，QIAO Haoyue1

（1. School of Civil Engineering，Tianjin University，Tianjin 300072，China;

2. Key Laboratory of Coast Civil Structure Safety （Tianjin University），Ministry of Education，Tianjin 300072，China;

3. Tianjin Municipal Engineering Design and Research Institute，Tianjin 300392，China）

Abstract：In order to investigate the influence of steel fiber content on fiber distribution and orientation in steel fiber reinforced self-compacting concrete，four kinds of concretes were prepared using four different fiber volume contents. The relationship between rheological properties of fresh concrete and fiber volume content was investigated and the fiber density in the cut planes of beam specimens was analyzed. The flow of fresh concrete with four different fiber volume contents was simulated by ANSYS CFX，where the effect of fiber volume content on the rheological properties was considered. Based on the velocity field of concrete obtained by simulation，the fiber is simplified as a number of particles that are rigidly connected and the motion of fibers is calculated by solving the rigid body dynamics equation. Through comparison between the experimental results，it is found that the proposed simulation method can determine the distribution and orientation of fiber immersed in the concrete. Furthermore，the simulation results show that the segregation degree of fiber in the vertical direction of beam decreases with the increase of fiber volume content. On the contrary，the orientation angle between fiber and beam axis increases.

Key words：fiber volume content;fiber distribution;fiber orientation;rheological properties of concrete;numerical simulation

眾所周知，混凝土的主要缺点是抗拉强度低，一旦发生开裂，在拉应力的作用下会急剧失去其承载能力. 这种弱点在很大程度上限制了普通混凝土在土木工程中的应用. 弥补此缺陷的一种有效方法是将适量的钢纤维掺入混凝土中. 纤维通过抵抗裂缝的形成和传播，提升了水泥基材料的延性、韧性和耗能能力[1-2]. 由于易于浇筑，钢纤维混凝土（SFRC）在不同的结构应用（例如工业地板，外部人行道，喷射混凝土和预制构件）中越来越多地替代了钢筋混凝土[3]. 如今，SFRC技术发展的新趋势是将自密实混凝土和SFRC相结合，后者被称为钢纤维自密实混凝土（SFRSCC）. 这种新型纤维水泥复合材料通过将自密实混凝土作为介质来输送钢纤维，为混凝土结构的设计和创新提供灵活性和便利性.

在过去的几十年中，许多学者致力于研究纤维特性对SFRC力学性能的影响. 纤维特性对SFRC的抗拉性能有着显著的影响，例如纤维类型、长径比、体积掺量以及分布取向等，具有不同纤维参数的SFRC表现出不同的力学性能[4]. 在纤维的各项特性中，增加纤维体积掺量是改善混凝土拉伸或弯曲性能最有效的方法. 在探究纤维体积掺量对SFRC的力学性能的影响时，大多数学者通常保持混凝土基体的配合比不变[5]，将纤维体积掺量作为唯一变量，而纤维体积掺量对新拌混凝土的流变性质有着重要的影响[6]，流变性质直接影响纤维的分布与取向[7]. 然而，已有研究往往会忽略因纤维掺量改变而引起的纤维分布与取向变化，但纤维的分布和取向对SFRC的力学性能有着至关重要的影响[8]. 因此，通过试验或数值模拟方法探究纤维分布与取向随纤维体积掺量的变化规律具有重要意义.

目前，用于检测硬化后混凝土基体内部纤维分布与取向的方法包括X射线法、电磁感应法[9]、图像处理技术以及电阻率测量法[10]等. 但是，这些方法需要复杂的数据分析过程，并且只能确定试件某个切割面上的纤维分布形态，很难应用到实际的工程结构中[11].数值模拟允许观察混凝土流动过程中纤维取向的变化，有助于深入理解新拌混凝土中的纤维取向与力学性能之间的关系， 但目前依然缺乏关于新拌混凝土流变性质对纤维分布和取向的影响的研究.

为此，本文配制了4种不同纤维体积掺量的纤维自密实混凝土，分析了纤维体积掺量与新拌混凝土的流变性质之间的关系. 借助软件ANSYS ?CFX模拟具有不同流变性质的混凝土的浇筑过程，基于模拟得到的混凝土速度场，将纤维视为刚性连接的多个球形粒子，采用刚体运动动力学方程计算了纤维的运动，分析了纤维体积掺量对纤维分布与取向的影响规律. 本文研究结果可为优化钢纤维混凝土的配合比提供相关依据.

1 ? 试验工况

1.1 ? 试件设计与制作

试验共设计了4组12个梁试件，共选取4种钢纤维体积掺量（0.4%、0.6%、0.8%、1%），每组包含3个试件，分别记为SF-0.4、SF-0.6、SF-0.8、SF-1.0，例如，SF-0.6表示钢纤维掺量为0.6%的梁试件. 试件为400 mm×100 mm×100 mm的棱柱体.

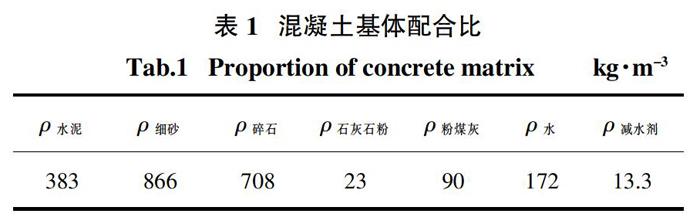
在只改变纤维体积掺量的情况下，保持混凝土基体成分比例不变，混凝土基体的组成如表1所示. 制作各试件所用的混凝土水灰比均为0.45，水泥标号为P.O 42.5R，骨料由细度模数为2.3的细砂与粒径为5～12 mm的碎石组成. 钢纤维采用长度为30 mm、截面直径为0.75 mm的长直纤维，抗拉强度为1 050 MPa. 为保证钢纤维均匀分布在混凝土中，首先对粗细骨料进行干拌，边搅拌边加入水泥及矿物参合料，再分批加入钢纤维进行拌和，加入80%的水和减水剂，搅拌数分钟后加入剩余的水，直到所有混合料拌和均匀后停止搅拌.

评价自密实混凝土的工作性能最常用的标准试验有V形漏斗试验、L形箱试验、U形箱试验、J环试验和坍落扩展度流动试验. 本文选用以上标准试验中的坍落扩展度试验与J环试验评价新拌混凝土的工作性能.

从模板的中心位置浇筑已拌好的混凝土，浇筑完成并在实验室环境中养护48 h后，拆除模板并在温度为20±2 ℃、相对湿度大于90%的环境下养护28 d. 养护完成后，对掺有纤维的各组试件进行切割，统计各切割面纤维数目以备试验.

1.2 ? 梁切割面上纤维数目的计算

沿每组梁试件的三个正交方向进行切割，纤维断面颜色与混凝土基体的颜色具有明显的差别，故通过人工计数的方法统计梁的三个正交切割面上的纤维根数，同时对纤维根数的计数过程重复数遍以排除由于测量导致的误差.梁三个正交切割面分别为垂直于梁轴向的横断面（α）、垂直于浇筑方向的竖断面（γ）以及平行于浇筑方向的纵断面（β），如图1所示. 此外，图2给出了切割面 上的钢纤维分布情况.

采用式（1）计算每个切割面上的纤维密度：

dn = ? ? ? ? ? （1）

式中：nf为切割面上纤维的总根数;Ac为切割面的面积. 各体积掺量下的纤维密度值取每组试件的平均值[12]，以体现试验结果的统计特征.

将切割面分为数个大小相等的正方形单元，计算每个单元中的纤维根数，采用纤维分散系数评价纤维的分散程度[13]，计算公式如下：

αf = exp

- ? ? ? ?（2）

式中：xi代表切割面上第i个分割单元中纤维的根数. αf值越接近于1，表明纤维在切割面上的分布越均匀.

2 ? 试验结果

2.1 ? 混凝土的流变性分析

图3给出了坍落扩展度和J环测试得到的新拌SFRSCC的流动结果. 表2给出了各组新拌混凝土坍落扩展度、J环扩展度以及T500（坍落至扩展直径为500 mm所需的时间）. 由表2可知，钢纤维的加入对自密实混凝土的T500和总流动时间具有显著的影响. 坍落扩展度随着钢纤维的体积掺量增加呈现逐渐减小的趋势，这是因为钢纤维的加入增加了混凝土的粘稠性，自密实混凝土的流动性能减弱，致使其扩展半径减小. 此外，相同钢纤维体积掺量下的坍落扩展度与J环扩展度的差值较小，表明各体积掺量下的钢纤维自密实混凝土具有良好的间隙通过能力. 总体上，各组SFRSCC均符合自密实混凝土的流动能力和通过能力的基本要求.

流变仪可以用来测量新拌混凝土的塑性黏度和屈服应力，但是对于相同的新拌混凝土，不同的流变仪给出不同的屈服应力和塑性黏度测量值. 因此，本文采用Ghanbari等[14]提出的黏度模型計算各组新拌混凝土的塑性黏度.

该模型考虑了钢纤维对混合物塑性黏度的影响，并已通过大量实验数据进行了验证. 预测塑性黏度的公式为：

μ = μ（1 - vf） + ? ? ? ? （3）

式中：μ为没有钢纤维的新拌混凝土的塑性黏度;vf为钢纤维体积掺量;re为钢纤维的长径比.

使用Roussel等[15]描述的分析方法计算了新拌混凝土的屈服应力. 该方法建立了坍落度试验与屈服应力之间的关系，屈服应力的计算公式为：

τy = ? ? ? ?（4）

式中：ρ为新拌混凝土的密度;H为新拌混凝土流动结束后的高度;R为新拌混凝土停止流动时半径.

基于混凝土工作性能试验结果，各组新拌混凝土的塑性黏度和屈服应力均由式（3）和式（4）计算得到. 表3列出了各组新拌混凝土的塑性黏度和屈服应力值. 新拌混凝土的流变性质与纤维的体积掺量之间的关系如图4所示. 结果表明，随着纤维体积掺量的增加，塑性黏度和屈服应力均呈线性增加. Alberti等[16]同样发现：增加纤维体积掺量会导致新拌混凝土的屈服应力和塑性黏度升高;流变参数与纤维的体积掺量之间的关系是线性的.

2.2 ? 纤维计数分析

表4给出了梁试件的三个正交切割面测得的平均纤维密度. 比较三个正交切割面上的纤维密度，可以发现平面α和平面γ中的纤维密度相似，均高于平面β中的纤维密度，表明纤维趋向于分布在平面 α和平面γ上，这是由于在浇筑过程中混凝土主要沿着水平面流动，而纤维的取向逐渐变得与流动方向一致. 此外，混凝土浇筑点位于模板中心，会导致α平面中的纤维密度较大.

注：括号中的数值为相应的标准差.

表5给出了不同体积掺量下切割面α上的分散系数值. 随着钢纤维体积掺量的提高，切割面α上的分散系数逐渐增大，表明钢纤维在切割面上的分布越来越均匀，这可归因于纤维掺量的增加改变了混凝土的流变性，进而导致纤维分布趋于均匀.

3 ? 基本理论

3.1 ? 新拌混凝土的本构方程

自密实混凝土被视为非牛顿流体，其流变行为通常由 Bingham 或 Herschel-Bulkley黏度模型来表征. 本文选用Bingham黏度模型用于模拟混凝土的流动，因为该模型的参数具有物理意义，并且比Herschel-Bulkley模型的参数更容易确定. Bingham的本构方程如下：

τ = μγ + τy ? ? ? ? （5）

式中：τ为剪应力;τy为屈服应力;μ为塑性黏度;γ为剪应变率.

3.2 ? 新拌混凝土的流动

新拌混凝土的流动模型基于均质方法，即将新拌混凝土视为一种均质的流体. 采用CFD软件CFX模拟新拌混凝土的流动，并求解流体质量和动量守恒的基本控制方程. 基本控制方程为：

[Δ]u = 0 ? ? ? ?（6）

+ [Δ]（ρu·u） = -[Δ]p + [Δ]τc + g ? ? ? ? ? ? ? （7）

式中：u为流体速度;ρ为流体密度;p为压强;τc为剪切力张量;g为重力加速度.

混凝土和空气之间的界面随时间而变化，因为新拌混凝土的流动是一个瞬态过程. 采用两相流VOF方法追踪混凝土的自由表面，VOF方法的基本思想是计算和更新各网格中混凝土和空气各占的体积掺量. 采用有限体积法（FVM）将整个计算域划分为网格，每个网格节点由给定大小的控制体积围绕，通过在每个控制体积上积分Navier-Stokes方程，从而获得一系列离散方程. 求解这些离散方程以计算混凝土的速度场，速度场用于更新空气和混凝土所占的体积掺量.

3.3 ? 钢纤维的处理

如果每根单独的纤维被视为单个球形颗粒，通过计算颗粒轨迹只能监测流动过程中该纤维的平动，而无法捕获纤维的取向. 为了监测纤维在流动过程中的取向，Kulasegaram等[17]使用一对距离等于纤维长度的球形颗粒代表单根纤维. 实际上，沿纤维长度的每个部分在流动过程中都会受到流体的作用力，因此，将纤维的运动简化为刚性连接的多个球形粒子的运动，能够更精确地考虑纤维的转动与平动. 图5给出了纤维的简化方法.

纤维被简化为多个刚性连接的球形粒子，纤维质量由各粒子平均分配. 因此，可将浸入混凝土中的纤维视为刚性细长杆，在流动过程中仅产生刚性运动，即转动和平动. 选取纤维的中心作为基本点，将纤维的运动分解为纤维相对于基点的旋转和基点的平移，采用刚体的一般动力学方程计算纤维的运动. 纤维的平动方程为：

mf ?= FD，i + Fg ? ? ?（8）

式中：mf 为单根纤维的质量;vf为纤维中点的速度; FD，i为第i个球形粒子的拖曳力;Fg为纤维受到的广义重力（包括浮力）.

计算球形粒子所受拖曳力的公式为：

FD = CD ρApup - v（up - v） ? ?（9）

式中：CD为粒子的拖曳力系数;Ap为粒子在流动方向的投影面积;up为与粒子相同位置处的新拌混凝土速度;v为粒子的速度. 需要注意的是，混凝土的速度是基于CFX软件中混凝土的速度场计算得到的，而CD由Haider等[18]提出的非球形粒子的阻力系數公式计算得到.

纤维的广义重力的计算公式如下：

Fg = mf

g ? ? ? （10）

纤维的转动方程为：

I· = T - ω × （I·ω） ? ? ?（11）

式中：I为纤维的惯性张量;ω为纤维的角速度;T为各粒子拖曳力对纤维中心的力矩之和.

T的计算公式如下：

T = FD，i × di ? ? ? ? ? （12）

式中：di为第i个球形粒子中心与纤维中心之间的距离.

根据上述计算过程，提出一种与CFD相结合的数值方法，用于监测计算域中所有纤维的位置. 考虑到计算时间与计算精度的平衡性，将每根纤维分为10个球形颗粒.

4 ? 数值方法验证

为了验证上述数值方法模拟纤维在自密实混凝土中运动的可行性，以本文试验中新拌混凝土的浇筑过程为对象进行验证.

4.1 ? 模型的建立

按照试件的实际尺寸，建立混凝土梁的数值模型，如图6所示. 为便于模拟结果的分析，对模型的三个轴进行统一的方向标定，Z轴为垂直于浇筑面的轴，X轴平行于梁模型主轴方向，Y轴为平行于试件短边的轴. 采用结构化网格划分方法，进行灵敏度分析，六面体网格边长确定为10 mm，网格总数为5 816个，基本实现计算精度和效率的平衡.

4.2 ? 边界条件及参数设置

各组新拌混凝土的屈服应力和塑性黏度采用表3中的数值，密度为2 255.3 kg/m3，空气视为密度为1.185 kg/m3、黏度为1.831 × 10-5的牛顿流体. 根据实验中混凝土浇筑点的位置，入口的边界条件采用速度边条，设置在模型上表面正中心处，尺寸为40 mm × 40 mm，浇筑速度为0.2 m/s，方向垂直于模型上表面. 出口边界条件采用开放压力边条（Opening），允许空气进入和离开计算域，计算域内外压力都设置为1个大气压，内外压力的差值为0. 由于混凝土可能在壁面附近滑动，因此对模板壁面施加有限滑移边界条件. 时间步长为0.01 s，计算总步数为1 250步，采用二阶隐式求解器，用迭代的方法计算流体质量和动量守恒的基本控制方程，以此来达到精确模拟的效果.

4.3 ? 纤维的生成

使用Mersenne-Twister程序在浇筑口正上方生成随机分布的纤维，该程序能生成均匀的伪随机值，从而纤维的位置和取向都是随机的.

各组新拌混凝土中纤维的总根数由式（13）计算得到：

Nf = ? ? ? ? ? （13）

式中：V为梁试件的体积;Vfib为单根纤维的体积.

在数值模拟过程中，纤维体积掺量为0.4%、0.6%、0.8%和1.0%对应的纤维总根数分别为1 207、1 811、2 414和3 018. 由于纤维掺量的变化，每种模拟工况中计算域纤维总根数是不同的，导致难以对比不同混凝土配合比下纤维的取向. 为了方便比较不同纤维体积掺量对应的纤维取向分布，采用纤维取向系数[19]分析纤维与梁主轴（X轴）之间的夹角分布. 取向系数计算公式为：

ηθ = cos θi ? ? ? （14）

式中：θi为纤维与梁主轴之间的夹角.

4.4 ? 纤维运动的求解流程

图7给出了计算纤维分布和取向的流程图. 首先，采用CFX获得新拌混凝土在每个时间步的速度場. 随后，在计算域的入口上方生成随机分布的纤维，纤维根据混凝土浇筑的总步数分批进入计算域中. 需要注意的是，每一时间步长中计算的纤维总数由上一步已经进入域中的纤维和本时间步内新进入域中的纤维组成. 基于CFX计算得到的速度场，计算每步进入域中纤维的运动，以确定纤维的位置和取向. 在下一时间步中，本步纤维的位置和取向作为已知值，进行循环运算. 最后，当步数达到1 250步，也就是混凝土浇筑完成时，所有纤维进入计算域，循环结束. 在Matlab中通过编程实现上述过程，时间步长同样为0.01 s.

4.5 ? 验证结果

模拟计算得到的纤维密度列于表6. 图8对比了试验和模拟获得的纤维分散系数值. 结果表明，通过数值模拟得到的纤维密度和纤维分散系数均与试验结果吻合较好，说明提出的数值方法能够模拟新拌混凝土流动过程中纤维的运动.

5 ? 模拟结果及分析

5.1 ? 纤维体积掺量对纤维分布的影响

首先将梁的数值模型在竖直方向（Z轴）上分为两部分，即下半梁和上半梁. 计算每部分的纤维根数，除以纤维总根数，通过纤维的相对含量分析纤维的竖向分布. 图9给出了不同纤维体积掺量下竖直方向上纤维的相对含量. 结果表明，梁下半部中的纤维相对含量多于梁上半部中的纤维相对含量，说明在混凝土浇筑过程中纤维发生了离析. 纤维离析主要是由于重力作用引起的. 另外，梁的上半部分和下半部分之间的纤维分布差异随着纤维体积掺量的增加而减小，两部分之间的纤维分布的差异值从38.4%减少到27.4%，这主要是因为增加纤维体积掺量会导致新鲜混合物的塑性黏度和屈服应力的增大，纤维与混凝土之间的黏聚力随之增强，进而减弱了纤维的离析程度. Hosseinpoor等[20]得出了类似的结论：增加新拌混凝土的塑性黏度和屈服应力会减少骨料在垂直方向上从水泥浆中的离析.

图10给出了不同纤维体积掺量下纤维在水平方向上的分布. 结果表明，纤维相对含量在梁跨中分布较多，在梁左右两端分布对称. 注意到有一个增加的趋势：越接近混凝土浇筑点，纤维数量越多，这种趋势主要由浇筑口的位置造成的，浇筑口下方纤维发生沉积，因而该处纤维数量较多.

5.2 ? 纤维体积掺量对纤维取向的影响

数值模拟得到的混凝土瞬态流动和纤维分布形态见图11和图12，此处仅给出了对应于0.4%和1.0%的纤维体积掺量的模拟结果. 由图11和图12可知，钢纤维被混凝土完全包裹. 纤维体积掺量为1.0%的混凝土界面的分层现象更为明显，因为纤维体积掺量较高的混凝土具有更大的黏度和屈服应力. 另外，越靠近壁面，纤维越趋于与壁面平行分布，这种取向趋势主要由混凝土的流速引起. 图13显示了距离梁底部0.02 m处水平面上混凝土速度的云图，可以看到混凝土的速度从壁面处最小值0 m/s组件增大到平面中心处的最大值. 因此，由于混凝土在水平面上存在速度差，壁面附近纤维逐渐与壁面对齐.

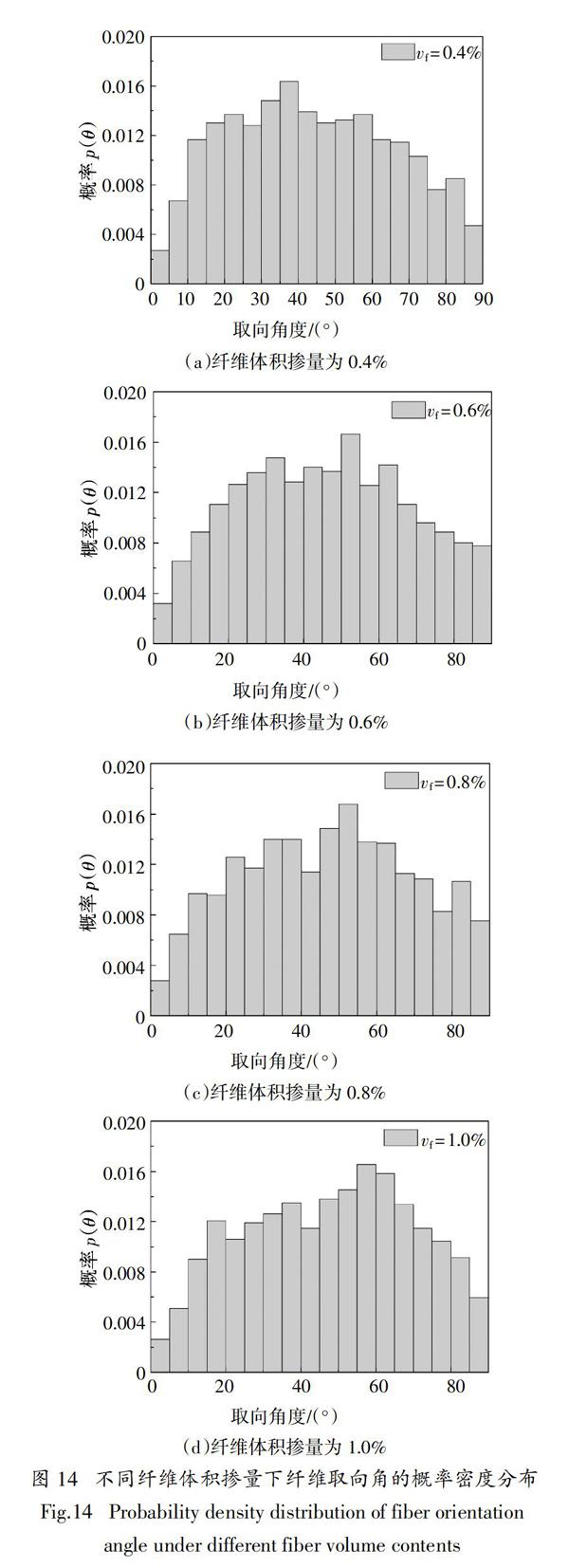
不同纤维体积掺量下纤维取向角的概率密度分布如图14所示，图中纤维取向角是基于域中所有纤维根数计算得到的，而不是针对某个切割面. 由图14可知，纤维体积掺量为0.4%对应的取向分布明显偏左，而纤维体积掺量为1.0%对应的取向直方图偏右分布，说明纤维取向角的平均值随纤维体积掺量的增加而增加，这同样是因为新拌混凝土的流变性质改变而导致的，即具有较低塑性黏度和屈服应力的新拌混凝土具有更好的流动性，纤维取向角在流场的作用下变得更小. 另一方面，纤维体积掺量为0.6%和0.8%对应的取向直方图均居中，但掺量为0.8%对应的取向分布比掺量为0.6%的略微偏右一些. 应该注意的是，角度分布在70°～ 90°之间的概率稍大于文献[21]对应的结果. 产生差异主要有两个原因：浇筑方法和试件的几何尺寸. 与从梁端部浇筑混凝土的结果相比，从梁中点位置浇筑混凝土会减少纤维的流动距离. 另一方面，试件的寬度（Y轴方向）比纤维的长度大许多，纤维能够自由旋转. 以上两点原因都可能增大纤维趋近于大角度的概率.

图15给出了纤维取向系数沿梁主轴（X轴）的变化. 由图15可知，跨中位置切割面上的纤维具有较大的取向系数，意味着纤维趋于与梁主轴平行分布. ?相反，梁两端的纤维均匀分布并且取向系数较小，这主要归因于梁中混凝土的流场与“壁面”效应，梁端部的壁面会使得端部区域的混凝土流动方向为自下而上，致使此区域的纤维与梁主轴之间的平均角度偏大，而梁跨中位置的混凝土水平地流向梁的两端，导致纤维具有较大的取向系数. 另一方面，随着纤维体积掺量的增加，各切割面上纤维系数逐渐减小.

6 ? 结 ? 论

1）纤维体积掺量是影响新拌混凝土流变性质的敏感因素，随着纤维体积掺量的增加，新拌混凝土的屈服应力和塑性黏度呈线性增加.

2）考虑纤维体积掺量对混凝土流变性质的影

响，采用CFX软件模拟新拌混凝土浇筑过程. 基于混凝土的速度场，利用Matlab编程求解纤维的运动方程，通过与试验结果对比证明了本文提出的模拟方法能够较好地确定纤维的分布与取向.

3）由于重力作用，不同纤维体积掺量下纤维都发生了离析，并且纤维的离析程度随着纤维体积掺量的增加而降低. 相反，纤维在梁的水平方向上基本均匀分布，只是在浇筑口处发生轻微沉积.

4）纤维体积掺量是影响纤维取向的关键因素，

纤维体积掺量越低，纤维与梁主轴之间倾斜角越小，梁各切割面上的纤维取向系数变大.

参考文献

[1] ? ?龚建清，周孜豪.纤维和外加剂对泡沫混凝土收缩性能的影响[J]. 湖南大学学报（自然科学版）：2019，46（5）：76—85.

GONG J Q，ZHOU Z H. Effects of fiber and admixture on shrinkage performance of foamed concrete[J]. ?Journal of Hunan University （Natural Sciences），2019，46（5）：76—85. （In Chinese）

[2] ? ?延潇，史庆轩，徐赵东. 钢纤维对混凝土与变形钢筋之间黏结性能试验研究[J]. 湖南大学学报（自然科学版），2020，47（1）：45—52.

YAN X，SHI Q X，XU Z D.Experimental study on bond behavior between concrete and deformed steel bar with different steel bar[J]. Journal of Hunan University （Natural Sciences），2020，47（1）：45—52. （In Chinese）

[3] ? ?赵国藩，彭少民，黄承逵. 钢纤维混凝土结构[M].北京：中国建筑工业出版社，1999：1—2.

ZHAO G F，PENG S M，HUANG C K. Steel fiber ?reinforced concrete structure [M]. Beijing：China Architecture & Building Press，1999：1—2. （In Chinese）

[4] ? ?YOO D Y，YOON Y S，BANTHIA N. Flexural response of steel-fiber-reinforced concrete beams：Effects of strength，fiber content，and strain-rate[J]. Cement and Concrete Composites，2015，64：84—92.

[5] ? ?LI B，XU L H，SHI Y C，et al. Effects of fiber type，volume fraction and aspect ratio on the flexural and acoustic emission behaviors of steel fiber reinforced concrete[J]. Construction and Building Materials，2018，181：474—486.

[6] ? ?GR?NEWALD S，WALRAVEN J C. Parameter-study on the influence of steel fibers and coarse aggregate content on the fresh properties of self-compacting concrete[J]. Cement and Concrete Research，2001，31（12）：1793—1798.

[7] ? ?BOULEKBACHE B，HAMRAT M，CHEMROUK M，et al. Flowability of fibre-reinforced concrete and its effect on the mechanical properties of the material[J]. Construction and Building Materials，2010，24（9）：1664—1671.

[8] ? ?ABRISHAMBAF A，BARROS J A O，CUNHA V M C F. Relation between fibre distribution and post-cracking behaviour in steel fibre reinforced self-compacting concrete panels[J]. Cement and Concrete Research，2013，51：57—66.

[9] ? ?TORRENTS J M，BLANCO A，PUJADAS P，et al. Inductive method for assessing the amount and orientation of steel fibers in concrete[J]. Materials and Structures，2012，45（10）：1577—1592.

[10] ?ALBERTI M G，ENFEDAQUE A，G?LVEZ J C. A review on the assessment and prediction of the orientation and distribution of fibres for concrete[J]. Composites Part B：Engineering，2018，151：274—290.

[11] ?DEEB R，KARIHALOO B L，KULASEGARAM S. Reorientation of short steel fibres during the flow of self-compacting concrete mix and determination of the fibre orientation factor[J]. Cement and Concrete Research，2014，56：112—120.

[12] ?GETTU R，GARDNER D R，SALD?VAR H，et al. Study of the distribution and orientation of fibers in SFRC specimens[J]. Materials and Structures，2005，38（1）：31—37.

[13] ?LEE B Y，KIM J K，KIM J S，et al. Quantitative evaluation technique of Polyvinyl Alcohol （PVA） fiber dispersion in engineered cementitious composites[J]. Cement and Concrete Composites，2009，31（6）：408—417.

[14] ?GHANBARI A，KARIHALOO B L. Prediction of the plastic viscosity of self-compacting steel fibre reinforced concrete[J]. Cement and Concrete Research，2009，39（12）：1209—1216.

[15] ?ROUSSEL N，COUSSOT P. “Fifty-cent rheometer” for yield stress measurements：From slump to spreading flow[J]. Journal of Rheology，2005，49（3）：705—718.

[16] ?ALBERTI M G，ENFEDAQUE A，G?LVEZ J C. The effect of fibres in the rheology of self-compacting concrete[J]. Construction and Building Materials，2019，219：144—153.

[17] ?KULASEGARAM S，KARIHALOO B L. Fibre-reinforced，self-compacting concrete flow modelled by smooth particle hydrodynamics[J]. Proceedings of the Institution of Civil Engineers - Engineering and Computational Mechanics，2013，166（1）：22—31.

[18] ?HAIDER A，LEVENSPIEL O. Drag coefficient and terminal velocity of spherical and nonspherical particles[J]. Powder Technology，1989，58（1）：63—70.

[19] ?WILLE K，TUE N V，PARRA-MONTESINOS G J. Fiber distribution and orientation in UHP-FRC beams and their effect on backward analysis[J]. Materials and Structures，2014，47（11）：1825—1838.

[20] ?HOSSEINPOOR M，KHAYAT K H，YAHIA A. Numerical simulation of self-consolidating concrete flow as a heterogeneous material in L-box set-up：Effect of rheological parameters on flow performance[J]. Cement and Concrete Composites，2017，83：290—307.

[21] ?ABRISHAMBAF A，PIMENTEL M，NUNES S. Influence of fibre orientation on the tensile behaviour of ultra-high performance fibre reinforced cementitious composites[J]. Cement and Concrete Research，2017，97：28—40.

编辑整理：科学技术创新杂志社编辑部 官方网站：www.hljkxzzs.com